Divisible and the Monoidal Quartet

November 12, 2021

A recent blog post by Gabriella Gonzalez, Co-Applicative programming style, has sparked discussion on ergonomic ways to make use of the Divisible type class. The conversation pointed to an interesting rabbit hole, and jumping into it resulted in these notes, in which I attempt to get a clearer view of picture of the constellation of monoidal functor classes that Divisible belongs to. The gist of it is that “Divisible is a contravariant Applicative, and Decidable is a contravariant Alternative” is not a full picture of the relationships between the classes, as there are a few extra connections that aren’t obvious to the naked eye.

Besides Gabriella’s post, which is an excellent introduction to Divisible, I recommend as background reading Tom Ellis’ Alternatives convert products to sums, which conveys the core intuition about monoidal functor classes in an accessible manner. There is a second post by Tom, The Mysterious Incomposability of Decidable, that this article will be in constant dialogue with, in particular as a source of examples. From now on I will refer to it as “the Decidable post”. Thanks to Gabriella and Tom for inspiring the writing of this article.

For those of you reading with GHCi on the side, the key general definitions in this post are available from this .hs file.

Applicative

As I hinted at the introduction, this post is not solely about Divisible, but more broadly about monoidal functor classes. To start from familiar ground and set up a reference point, I will first look at the best known of those classes, Applicative. We won’t, however, stick with the usual presentation of Applicative in terms of (<*>), as it doesn’t generalise to the other classes we’re interested in. Instead, we will switch to the monoidal presentation: ¹

zipped :: Applicative f => f a -> f b -> f (a, b)
zipped = liftA2 (,)

-- An operator spelling, for convenience.
(&*&) :: Applicative f => f a -> f b -> f (a, b)
(&*&) = zipped
infixr 5 &*&

unit :: Applicative f => f ()
unit = pure ()

-- Laws:

-- unit &*& v ~ v
-- u &*& unit ~ u
-- (u &*& v) &*& w ~ u &*& (v &*& w)

(Purely for the sake of consistency, I will try to stick to the Data.Functor.Contravariant.Divisible naming conventions for functions like zipped.)

The matter with (<*>) (and also liftA2) that stops it from being generalised for our purposes is that it leans heavily on the fact that Hask is a Cartesian closed category, with pairs as the relevant product. Without that, the currying and the partial application we rely on when writing in applicative style become unfeasible.

While keeping ourselves away from (<*>) and liftA2, we can recover, if not the full flexibility, the power of applicative style with a variant of liftA2 that takes an uncurried function:

lizip :: Applicative f => ((a, b) -> c) -> f a -> f b -> f c
lizip f u v = fmap f (zipped u v)

(That is admittedly a weird name; all the clashing naming conventions around this topic has left me with few good options.)

On a closing note for this section, my choice of operator for zipped is motivated by the similarity with (&&&) from Control.Arrow:

(&&&) :: Arrow p => p a b -> p a c -> p a (b, c)

In particular, (&*&) for the function Applicative coincides with (&&&) for the function Arrow.

Leaning on connections like this one, I will use Control.Arrow combinators liberally, beginning with the definition of the following two convenience functions that will show up shortly:

dup :: a -> (a, a)
dup = id &&& id

forget :: Either a a -> a
forget = id ||| id

Divisible

As summarised at the beginning of the Decidable post, while Applicative converts products to products covariantly, Divisible converts products to products contravariantly. From that point of view, I will take divided, the counterpart to zipped, as the fundamental combinator of the class:

-- This is the divided operator featured on Gabriella's post, soon to
-- become available from Data.Functor.Contravariant.Divisible
(>*<) :: Divisible k => k a -> k b -> k (a, b)
(>*<) = divided
infixr 5 >*<

-- Laws:

-- conquered >*< v ~ v
-- u >*< conquered ~ u
-- (u >*< v) >*< w ~ u >*< (v >*< w)

Recovering divide from divided is straightforward, and entirely analogous to how lizip can be obtained from zipped:

divide :: Divisible k => (a -> (b, c)) -> k b -> k c -> k a
divide f = contramap f (divided u v)

Lessened currying aside, we might say that divide plays the role of liftA2 in Divisible.

It’s about time for an example. For that, I will borrow the one from Gabriella’s post:

data Point = Point { x :: Double, y :: Double, z :: Double }
    deriving Show

nonNegative :: Predicate Double
nonNegative = Predicate (0 <=)

-- (>$<) = contramap
nonNegativeOctant :: Predicate Point
nonNegativeOctant =
    adapt >$< nonNegative >*< nonNegative >*< nonNegative
    where
    adapt = x &&& y &&& z

The slight distortion to Gabriella’s style in using (&&&) to write adapt pointfree is meant to emphasise how that deconstructor can be cleanly assembled out of the component projection functions x, y and z. Importantly, that holds in general: pair-producing functions a -> (b, c) are isomorphic (a -> b, a -> c) pairs of projections. That gives us a variant of divide that takes the projections separately:

tdivide :: Divisible k => (a -> b) -> (a -> c) -> k b -> k c -> k a
tdivide f g u v = divide (f &&& g) u v

Besides offering an extra option with respect to ergonomics, tdivide hints at extra structure available from the Divisible class. Let’s play with the definitions a little:

tdivide f g u v
divide (f &&& g) u v
contramap (f &&& g) (divided u v)
contramap ((f *** g) . dup) (divided u v)
(contramap dup . contramap (f *** g)) (divided u v)
contramap dup (divided (contramap f u) (contramap g v))
divide dup (contramap f u) (contramap g v)

divide dup, which duplicates input in order to feed each of its arguments, is a combinator worthy of a name, or even two:

dplus :: Divisible k => k a -> k a -> k a
dplus = divide dup

(>+<) :: Divisible k => k a -> k a -> k a
(>+<) = dplus
infixr 5 >+<

So we have:

tdivide f g u v = dplus (contramap f u) (contramap g v)

Or, using the operators:

tdivide f g u v = f >$< u >+< g >$< v

An alternative to using the projections to set up a deconstructor to be used with divide is to contramap each projection to its corresponding divisible value and combine the pieces with (>+<). That is the style favoured by Tom Ellis, ² which is why I have added a “t” prefix to tdivide comes from. For instance, Gabriella Gonzalez’s example would be spelled as follows in this style:

nonNegativeOctantT :: Predicate Point
nonNegativeOctantT =
    x >$< nonNegative >+< y >$< nonNegative >+< z >$< nonNegative

Alternative

The (>+<) combinator defined above is strikingly similar to (<|>) from Alternative, down to its implied monoidal nature: ³

(>+<) :: Divisible k => k a -> k a -> k a

(<|>) :: Alternative f => f a -> f a -> f a

It is surprising that (>+<) springs forth in Divisible rather than Decidable, which might look like the more obvious candidate to be Alternative’s contravariant counterpart. To understand what is going on, it helps to look at Alternative from the same perspective we have used here for Applicative and Divisible. For that, first of all we need an analogue to divided. Let’s borrow the definition from Applicatives convert products to sums:

combined :: Alternative f => f a -> f b -> f (Either a b)
combined u v = Left <$> u <|> Right <$> v

(-|-) :: Alternative f => f a -> f b -> f (Either a b)
(-|-) = combined
infixr 5 -|-

-- We also need a suitable identity:
zero :: Alternative f => f Void
zero = empty

-- Laws:

-- zero -|- v ~ v
-- u -|- zero ~ u
-- (u -|- v) -|- w ~ u -|- (v -|- w)

(I won’t entertain the various controversies about the Alternative laws here, nor any interaction laws involving Applicative. Those might be interesting matters to think about from this vantage point, though.)

A divide analogue follows:

combine :: Alternative f => (Either a b -> c) -> f a -> f b -> f c
combine f u v = fmap f (combined u v)

Crucially, Either a b -> c can be split in a way dual to what we have seen earlier with a -> (b, c): an Either-consuming function amounts to a pair of functions, one to deal with each component. That being so, we can use the alternative style trick done for Divisible by dualising things:

tcombine :: Alternative f => (a -> c) -> (b -> c) -> f a -> f b -> f c
tcombine f g = combine (f ||| g)

tcombine f g u v
combine (f ||| g) u v
fmap (f ||| g) (combined u v)
fmap (forget . (f +++ g)) (combined u v)
fmap forget (combined (fmap f u) (fmap g v))
combine forget (fmap f u) (fmap g v)

To keep things symmetrical, let’s define:

aplus :: Alternative f => f a -> f a -> f a
aplus = combine forget
-- (<|>) = aplus

So that we end up with:

tcombine f g u v = aplus (fmap f u) (fmap g v)

tcombine f g u v = f <$> u <|> g <$> v

For instance, here is the Alternative composition example from the Decidable post…

alternativeCompose :: [String]
alternativeCompose = show <$> [1,2] <|> reverse <$> ["hello", "world"]

… and how it might be rendered using combine/(-|-):

alternativeComposeG :: [String]
alternativeComposeG = merge <$> [1,2] -|- ["hello", "world"]
    where
    merge = show ||| reverse

There is, therefore, something of a subterranean connection between Alternative and Divisible. The function arguments to both combine and divide, whose types are dual to each other, can be split in a way that not only reveals an underlying monoidal operation, (<|>) and (>+<) respectively, but also allows for a certain flexibility in using the class combinators.

Decidable

Last, but not least, there is Decidable to deal with. Data.Functor.Contravariant.Divisible already provides chosen as the divided analogue, so let’s just supply the and operator variant: ⁴

(|-|) :: Decidable k => k a -> k b -> k (Either a b)
(|-|) = chosen
infixr 5 |-|

-- Laws:

-- lost |-| v ~ v
-- u |-| lost ~ u
-- (u |-| v) |-| w ~ u |-| (v |-| w)

choose can be recovered from chosen in the usual way:

choose :: Decidable k => (a -> Either b c) -> k b -> k c -> k a
choose f u v = contamap f (chosen u v)

The a -> Either b c argument of choose, however, is not amenable to the function splitting trick we have used for divide and combine. Either-producing functions cannot be decomposed in that manner, as the case analysis to decide whether to return Left or Right cannot be disentangled. This is ultimately what Tom’s complaint about the “mysterious incomposability” of Decidable is about. Below is a paraphrased version of the Decidable example from the Decidable post:

data Foo = Bar String | Baz Bool | Quux Int
    deriving Show

pString :: Predicate String
pString = Predicate (const False)

pBool :: Predicate Bool
pBool = Predicate id

pInt :: Predicate Int
pInt = Predicate (>= 0)

decidableCompose :: Predicate Foo
decidableCompose = analyse >$< pString |-| pBool |-| pInt
    where
    analyse = \case
        Bar s -> Left s
        Baz b -> Right (Left b)
        Quux n -> Right (Right n)

The problem identified in the post is that there is no straightfoward way around having to write “the explicit unpacking into an Either” performed by analyse. In the Divisible and Alternative examples, it was possible to avoid tuple or Either shuffling by decomposing the counterparts to analyse, but that is not possible here. ⁵

In the last few paragraphs, we have mentioned Divisible, Alternative and Decidable. What about Applicative, though? The Applicative example from the Decidable post is written in the usual applicative style:

applicativeCompose :: [[String]]
applicativeCompose =
    f <$> [1, 2] <*> [True, False] <*> ["hello", "world"]
    where
    f = (\a b c -> replicate a (if b then c else "False"))

As noted earlier, though, applicative style is a fortunate consequence of Hask being Cartesian closed, which makes it possible to turn (a, b) -> c into a -> b -> c. If we leave out (<*>) and restrict ourselves to (&*&), we end up having to deal explicitly with tuples, which is a dual version of the Decidable issue:

monoidalCompose :: [[String]]
monoidalCompose =
    consume <$> [1, 2] &*& [True, False] &*& ["hello", "world"]
    where
    consume (a, (b, c)) = replicate a (if b then c else "False")

Just like a -> Either b c functions, (a, b) -> c functions cannot be decomposed: the c value can be produced by using the a and b components in arbitrary ways, and there is no easy way to disentangle that.

Decidable, then, relates to Applicative in an analogous way to how Divisible does to Alternative. There are a few other similarities between them that are worth pointing out:

• Neither Applicative nor Decidable offer a monoidal f a -> f a -> f a operation like the ones of Alternative and Decidable. A related observation is that, for example, Op’s Decidable instance inherits a Monoid constraint from Divisible but doesn’t actually use it in the method implementations.

• choose Left and choose Right can be used to combine consumers so that one of them doesn’t actually receive input. That is analogous to how (<*) = lizip fst and (*>) = lizip snd combine applicative values while discarding the output from one of them.

• Dually to how zipped/&*& for the function functor is (&&&), chosen for decidables such as Op and Predicate amounts to (|||). My choice of |-| as the corresponding operator hints at that.

In summary

To wrap things up, here is a visual summary of the parallels between the four classes:

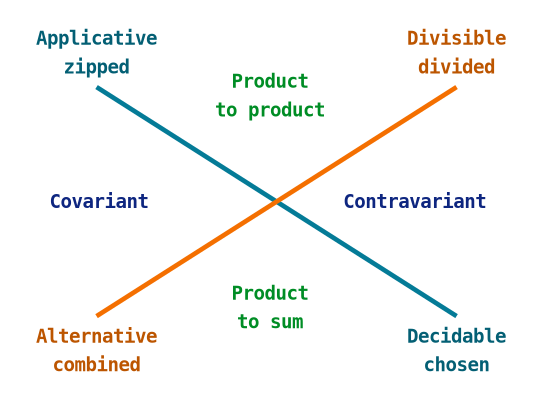
To my eyes, the main takeaway of our figure of eight trip around this diagram has to do with its diagonals. Thanks to a peculiar kind of duality, classes in opposite corners of it are similar to each other in quite a few ways. In particular, the orange diagonal classes, Alternative and Divisible, have monoidal operations of f a -> f a -> f a signature that emerge from their monoidal functor structure.

That Divisible, from this perspective, appears to have more to do with Alternative than with Applicative leaves us a question to ponder: what does that mean for the relationship between Divisible and Decidable? The current class hierarchy, with Decidable being a subclass of Divisible, mirrors the Alternative-Applicative relationship on the other side of the covariant-contravariant divide. That, however, is not the only reasonable arrangement, and possibly not even the most natural one. ⁶

Appendixes

dplus is a monoidal operation

If we are to show that (>+<) is a monoidal operation, first of all we need an identity for it. conquer :: f a sounds like a reasonable candidate. It can be expressed in terms of conquered, the unit for divided, as follows:

-- conquer discards input.
conquer = const () >$< conquered

The identity laws do come out all right:

conquer >+< v = v  -- Goal
conquer >+< v  -- LHS
dup >$< (conquer >*< v)
dup >$< ((const () >$< conquered) >*< v)
dup >$< (first (const ()) >$< (conquered >*< v))
first (const ()) . dup >$< (conquered >*< v)
-- conquered >*< v ~ v
first (const ()) . dup >$< (snd >$< v)
snd . first (const ()) . dup >$< v
v  -- LHS = RHS

u >+< conquer = u  -- Goal
u >+< conquer  -- LHS
dup >$< (u >*< discard)
dup >$< (u >*< (const () >$< conquered))
dup >$< (second (const ()) >$< (u >*< conquered))
second (const ()) . dup >$< (u >*< conquered)
-- u >*< conquered ~ u
second (const ()) . dup >$< (fst >$< u)
fst . second (const ()) . dup >$< u
u  -- LHS = RHS

And so does the associativity one:

(u >+< v) >+< w = u >+< (v >+< w)  -- Goal
(u >+< v) >+< w  -- LHS
dup >$< ((dup >$< (u >*< v)) >*< w)
dup >$< (first dup >$< ((u >*< v) >*< w))
first dup . dup >$< ((u >*< v) >*< w)
u >+< (v >+< w)  -- RHS
dup >$< (u >*< (dup >$< (v >*< w)))
dup >$< (second dup >$< (u >*< (v >*< w)))
second dup . dup >$< (u >*< (v >*< w))
-- (u >*< v) >*< w ~ u >*< (v >*< w)
-- assoc ((x, y), z) = (x, (y, z))
second dup . dup >$< (assoc >$< ((u >*< v) >*< w))
assoc . second dup . dup >$< ((u >*< v) >*< w)
first dup . dup >$< ((u >*< v) >*< w)  -- LHS = RHS

Handling nested Either

The examples in this appendix are available as a separate .hs file.

There is a certain awkwardness in dealing with nested Either as anonymous sums that is hard to get rid of completely. Prisms are a tool worth looking into in this context, as they are largely about expressing pattern matching in a composable way. Let’s bring lens into Tom’s Decidable example, then:

data Foo = Bar String | Baz Bool | Quux Int
    deriving (Show)
makePrisms ''Foo

A cute trick with prisms is using outside to fill in the missing cases of a partial function (in this case, (^?! _Quux):

anonSum :: APrism' s a -> (s -> b) -> s -> Either a b
anonSum p cases = set (outside p) Left (Right . cases)

decidableOutside :: Predicate Foo
decidableOutside = analyse >$< pString |-| pBool |-| pInt
    where
    analyse = _Bar `anonSum` (_Baz `anonSum` (^?! _Quux))

An alternative is using matching to write it in a more self-explanatory way:

matchingL :: APrism' s a -> s -> Either a s
matchingL p = view swapped . matching p

decidableMatching :: Predicate Foo
decidableMatching =
    choose (matchingL _Bar) pString $
    choose (matchingL _Baz) pBool $
    choose (matchingL _Quux) pInt $
    error "Missing case in decidableMatching"

These implementations have a few inconveniences of their own, the main one perhaps being that there is noting to stop us from forgetting one of the prisms. The combinators from the total package improve on that by incorporating exhaustiveness checking for prisms, at the cost of requiring the sum type to be defined in a particular way.

There presumably also is the option of brining in heavy machinery, and setting up an anonymous sum wrangler with Template Haskell or generics. In fact, it appears the shapely-data package used to offer precisely that. It might be worth it to take a moment to make it build with recent GHCs.

All in all, these approaches feel like attempts to approximate extra language support for juggling sum types. As it happens, though, there is a corner of the language which does provide extra support: arrow notation. Converting the example to arrows provides a glimpse of what might be:

-- I'm going to play nice, rather than making b phantom and writing a
-- blatantly unlawful Arrow instance just for the sake of the notation.
newtype Pipecate a b = Pipecate { getPipecate :: a -> (Bool, b) }

instance Category Pipecate where
    id = Pipecate (True,)
    Pipecate q . Pipecate p = Pipecate $ \x ->
        let (bx, y) = p x
            (by, z) = q y
        in (bx && by, z)

instance Arrow Pipecate where
    arr f = Pipecate (const True &&& f)
    first (Pipecate p) = Pipecate $ \(x, o) ->
         let (bx, y) = p x
         in (bx, (y, o))

instance ArrowChoice Pipecate where
    left (Pipecate p) = Pipecate $ \case
        Left x ->
            let (bx, y) = p x
            in (bx, Left y)
        Right o -> (True, Right o)

fromPred :: Predicate a -> Pipecate a ()
fromPred (Predicate p) = Pipecate (p &&& const ())

toPred :: Pipecate a x -> Predicate a
toPred (Pipecate p) = Predicate (fst . p)

decidableArrowised :: Predicate Foo
decidableArrowised = toPred $ proc foo -> case foo of
    Bar s -> fromPred pString -< s
    Baz b -> fromPred pBool -< b
    Quux n -> fromPred pInt -< n

decidableArrowised corresponds quite closely to the various Decidable-powered implementations. Behind the scenes, case commands in arrow notation give rise to nested eithers. Said eithers are dealt with by the arrows, which are combined in an appropriate way with (|||). (|||), in turn, can be seen as an arrow counterpart to chosen/(|-|). Even the -< “feed” syntax, which the example above doesn’t really take advantage of, amounts to slots for contramapping. If someone ever feels like arranging a do-esque noation for Decidable to go with Gabriella’s DivisibleFrom, it seems case commands would be a nice starting point.